Ett välkänt teorem säger att om man inte har några problem så lyckas man ändå skaffa sig några. Jag har ju tidigare snuddat vid schackproblemkonsten vid några tillfällen, till exempel då jag skrev om den binära flecken, när jag presenterade död räkning och nu senast då jag gratulerade David Aler på sin 60-årsdag, med ett egenhändigt komponerat schackproblem, minsann.
Vad har jag ställt till med nu då? Jo, jag råkade på facebook kommentera ett problem som innehöll ett enpassant-slag, och någon undrade vad »schacketiketten» hade för åsikt om sådana problem. Så här är det[1]:
Ett enpassant-slag är tillåtet endast om man kan bevisa att en bonde i draget innan diagramställningen utfört ett dubbelsteg som möjliggör slag en passant.
För rockad gäller däremot att den är tillåten om man inte kan bevisa att endera kungen eller det aktuella tornet måste ha flyttat för att den aktuella ställningen ska kunnat uppstå.
Jag påpekade också att jag hade sett ett problem som utnyttjade dessa konventioner på ett intressant sätt, och här sitter jag nu för att försöka göra en blogga av det hela. Men innan jag tar itu med det problemet, som jag faktiskt lyckats hitta, så tänkte jag visa ett par andra problem som utnyttjar ovanstående regler.
Det första står min före detta klubbkamrat i LASS, Åke Hellström, för. 1948 gjorde han ett problem som enligt Börje Pettersson i LASSmeddelande 1990/2 orsakade ett mindre lösaruppror bland Dalademokratens läsare; så här såg hans problem ut[2]:


























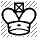





































Åke Hellström, Dalademokraten 1948
Det här är ett exempel på en ganska enkel bevisföring; svarts kung kan ju inte ha rört på sig i sista draget, och bonden måste ha tagit ett dubbelsteg, annars hade vits kung varit schackad. Efter 1. axb6 ep sätter vit matt inom de angivna tre dragen, men utan enpassant-slaget tar det längre tid.
Raymond Smullyan var en problemmakare av rang, och jag har ett flertal av hans tidiga böcker. I en av dem ställs Sherlock Holmes inför frågan »Går det att konstruera en schackställning där man kan bevisa att vit kan sätta matt i två drag, men det inte går att ange de drag som leder fram till matten?» Det här är den ställning som Smullyan hade i åtanke[3]:








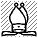























































Raymond Smullyan, The chess mysteries of Sherlock Holmes
Återigen handlar det om vad draget innan diagramställningen var — om kungen eller tornet flyttade spelar vit helt enkelt 1. Ke6 och följer upp med 2. g8D, eftersom svart inte kan rockera. Har bonden däremot tagit ett dubbelsteg kan vit i stället börja med 1. dxe6 ep och bemöta 1… 0-0-0 med 2. b7[4]. Här töjer alltså Smullyan lite på reglerna, eftersom han faktiskt inte kan bevisa vare sig att enpassantslaget är möjligt eller att rockaden är omöjlig. Men det må vara historiens förmodligen främste skapare av logiska gåtor förlåtet. Han blev en gång presenterad inför en föreläsning med ungefär de här orden[5]: »Professor Smullyan kommer i sin föreläsning att visa att endera existerar inte ni, eller så existerar inte han, men ni har ingen möjlighet att veta vilket…»
Så, äntligen till det problem som jag mindes. Betingelsen för dess a-del är föga uppseendeväckande, hjälpmatt i tre drag, sådana går det minst tretton på dussinet. Men b-delens betingelse är desto märkligare; den ställning som det handlar om är den som uppstår efter första draget av både svart och vit, och nu är betingelsen hjälpmatt i två drag. Den som tänker att det borde väl bara vara att fortsätta med resterande drag i lösningen från a-delen är i högsta grad ursäktad, men här sker det mirakulösa att den lösningen inte längre fungerar, medan det däremot uppenbarar sig en annan. Så här går det till:
































































Jan Hein Verduin, Thema Danicum, okt. 2000
Det borde inte vara så svårt att lösa den med alla ledtrådar som jag slösat härovan, men här kommer i alla fall lösningen: 1. Ke8+ g4 2. fxg3+ ep Kg2 3. Ld7 Tf8 matt.
Men låt oss ta en särskild titt på b-delen:
































































Jan Hein Verduin, Thema Danicum, okt. 2000
Här ser man först att den »gamla» lösningen inte fungerar — i den här ställningen, berövad sin historia från de första dragen, går det inte att bevisa att vit just spelat g4, och därmed är enpassant-slaget inte tillåtet. Men samtidigt står nu kung och torn på sina utgångsrutor, och det går inte heller att bevisa att de måste ha rört på sig! Alltså har vi lösningen 1. Ld7 Txb3 2. 0-0-0 Se7 matt.
Visst var det väl lite vitsigt?
Fotnoter:
- Den som inte tror mig kan leta rätt på relevant information på Wikipedia; den som inte tror på Wikipedia heller får väl utarbeta en egen etikett. [↩]
- Addendum 2019-09-28: Den skarpögde problemexperten Kaj Engström upptäckte att problemet i sin tidigare publicerade form var bilösligt, vilket visade sig bero på att bonden råkat halka en linje fel; den ska stå på d-linjen, och inte på e. Jag ber Åke, Kaj och alla andra om ursäkt för mitt slarv. Addendum 2019-09-28, några timmar senare: Kaj var ändå inte nöjd, och det med rätta; det finns ju inget som hindrar att svart slagit cxb5… Med hjälp av Robert Ericsson och en artikel han skrivit om Åke Hellström och hans schackproblem kan nu slås fast att bonden halkat två steg fel; ett då vi publicerade det i LASSmeddelande 1991/1-2 (sid 38; det var där jag tittade när jag skrev kommentaren ovan), och ett när jag satte ihop den här bloggan; bonden ska alltså stå på c-linjen, och inte på d eller e. Denna digitalt halkande bonde får mig osökt (?) att tänka på några ord från Nåd och onåd av Bodil Malmsten: »Digital istid — flytande kristall»… Det återstår bara att återigen be Åke, Kaj (som hela tiden föreslog att bonden skulle stå på c6) och alla andra om ursäkt. [↩]
- Det är dock inte den ställning som står i min upplaga av boken — där återfinns en vit bonde på a7, vilket förstör hela poängen. [↩]
- Med en bonde på a7 leder ju 1. Ke6 0-0-0 också till matt med 2. a8D [↩]
- Tyvärr hittar jag inte det exakta citatet i hastigheten; om jag gör det kommer jag att ändra i texten, så ni bara vet… Addendum 2019-11-03: Jag hittade citatet på webben; det är dock såpass nära min ursprungliga text att jag inte ser någon anledning att ändra den. [↩]
