För någon vecka sedan uppmärksammade mig Olle Häggström på att Magnus Carlsen missade en möjlighet till odödlighet[1]. Olle tänkte på denna ställning från det fjärde partiet i matchen mot Anand:












































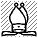

















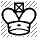

Ställning efter svarts 15:e drag
och menade att Carlsen här kunde prövat 16. Sb3 med idén Sbd2, Sd4 och S2f3; en intressant springarmanöver som både Olle och jag har praktiserat genom åren. Att denna strategi har ett visst mått av giftighet visades inte minst i det elfte matchpartiet, där Magnus var nöjd med att bara skyffla runt sina pjäser i väntan på att svart skulle implodera. Det är emellertid möjligt att denna plan är mer effektiv i ett läge där motståndaren känner sig förpliktigad att företa sig något.
I en fotnot till mitt opus föreslog jag ett namn på denna manöver »tills vetenskapen funnit ännu tidigare exempel». Redan då hyste jag vissa planer på utföra den »vetenskapliga» undersökningen; och nu har jag äntligen lyckats få den ökända kroppsdelen ur fordonet. Men innan jag presenterar mina resultat kommer jag att, i något slags vetenskaplig anda, ägna ett kapitel åt att lägga fast den terminologi jag tänker använda och ett åt att beskriva hur jag gjort, ifall någon skulle vilja repetera eller utvidga min forskning. Den otålige som bara är intresserad av att se exempel på denna spännande manöver gör nog bäst i att hoppa direkt till resultaten.
Terminologi
Låt mig först definiera den manöver vi letar efter:
I en viss ställning har en spelare två springare på rutorna A respektive B. Fyra drag senare har de båda springarna bytt plats, så att den som ursprungligen stod på ruta A nu står på ruta B, och vice versa.
Efter en myckenhet grubblande har jag bestämt mig för att kalla denna manöver för en FSPW, vilket bör utläsas Fyrdragig SpringarPlatzWechsel. Platzwechsel är redan ett begrepp inom problemschacket[2]; »Springar-» och »Fyrdragig» är prefix som måste tillsättas för att skala bort liknande manövrer som endera utförs av andra pjäser eller tar längre tid på sig[3].
Det finns sex grundtyper av rutpar (A och B) som kan utgöra utgångspunkt för ovanstående manöver, och de har markerats i nedanstående diagram; A är i detta fallet d4, medan B kan vara någon av de rutor som indikerats med en chockrosa springare. Med hjälp av translationer och speglingar horisontellt, vertikalt eller diagonalt kan man sedan skapa alla springarkonstellationer som kan vara utgångspunkt för en FSPW.
































































Som man lätt inser från ovanstående diagram finns det två olika typer av utgångsställningar beroende på om fältet B har samma färg som A eller ej; om A och B har samma färg så kommer jag att prata om en »symmetrisk» FSPW, om de har olika färg talar jag i stället om en »asymmetrisk» FSPW. Namnen beror på att i det första fallet gör båda springarna två drag var, medan i det andra tvingas en pålle att utföra tre hopp medan den andra bara gör ett.
Ännu en bit terminologi, denna gång relaterad till den figur som springarna ritar upp under sin ringdans. Jag har gett de fem olika utgångsställningarna i det symmetriska fallet prefixen »kort rak» (f4), »lång rak» (h4), »kort diagonal» (e3), »lång diagonal» (g1) och »kamelstegs» (g3); namnen borde vara i stort sett självförklarande, åminstone för dem som är bekanta med fantasipjäsen kamels rörelsemönster. De asymmetriska FSPW-manövrerna kan klassificeras med samma termer och på samma sätt om man i stället för utgångsställningen använder den konfiguration som uppstår efter det första draget i serien[4].
Metod
Som material att söka i använde jag en gammal och bamsig samlingsfil som jag totat ihop i slutet av 90-talet; de senaste tillskotten gjordes nog i början av 00-talet, så den är ingalunda »up-to-date». Den består av några större databaser från CD-ROM (bland annat FatBase), några större databaser från internet samt diverse slattar från alla möjliga och omöjliga håll; sammanlagt handlar det om omkring 4.9 miljoner partier, som när de kavlats ut i textformat (PGN) upptar ca 3.2 GByte.
För att söka i denna massiva datamängd använde jag ett program speciellt ägnat åt avancerade sökningar i schackdatabaser, CQL. Det program jag skrev utnyttjade en av dess nyaste finesser, »tags», vilket kort uttryckt gör det möjligt att följa upp var en viss pjäs befinner sig på brädet. Efter några försök beslöt jag mig för en tvåstegsraket — först körde jag partierna genom ett grovfilter som gallrade bort allt utom möjliga kandidater till FSPW:er, och sedan ett betydligt långsammare men noggrannare filter som sållade fram guldkornen. Det första programmet ser ut så här:
(match :pgn big1.pgn :output tmp1.pgn :forany Kn1 [N] :forany Kn2 [N] (position :shift :flip :sequence ((position $Kn1[d4] $Kn2[f3,e3,f4,h4,g3,g1]) (position) (position) (position) (position) (position) (position) (position $Kn1[f3,e3,f4,h4,g3,g1] $Kn2[d4]) ); end sequence ); end position ); end match
I korthet letar det här programmet fram alla partier där en springare i utgångsställningen stått på en viss ruta, och fyra drag senare står på någon av sex bestämda rutor, medan en annan häst gjort samma tripp åt andra hållet. Här finns alltså ingen kontroll av att det är samma fält det handlar om i klungan av sex rutor, utan vilket fält som helst duger. Det ger naturligtvis ganska många falska träffar, men om big1.pgn innehöll ungefär en miljon partier hamnade tmp1.pgn någonstans runt 5-6000 partier.
Det andra program jag skrev ser ut så här:
(match
:pgn tmp1.pgn
:output out1.pgn
:forany Kn1 [N]
:forany Kn2 [N]
(position
:or
(
(position
:shift :flip
:sequence
((position $Kn1[d4] $Kn2[f3])
(position)
(position)
(position)
(position)
(position)
(position)
(position $Kn1[f3] $Kn2[d4])
)
)
(position
:shift :flip
:sequence
((position $Kn1[d4] $Kn2[h4])
(position)
(position)
(position)
(position)
(position)
(position)
(position $Kn1[h4] $Kn2[d4])
)
)
(position
:shift :flip
:sequence
((position $Kn1[d4] $Kn2[e3] )
(position)
(position)
(position)
(position)
(position)
(position)
(position $Kn1[e3] $Kn2[d4])
)
)
(position
:shift :flip
:sequence
((position $Kn1[d4] $Kn2[f4] )
(position)
(position)
(position)
(position)
(position)
(position)
(position $Kn1[f4] $Kn2[d4])
)
)
(position
:shift :flip
:sequence
((position $Kn1[d4] $Kn2[g1] )
(position)
(position)
(position)
(position)
(position)
(position)
(position $Kn1[g1] $Kn2[d4])
)
)
(position
:shift :flip
:sequence
((position $Kn1[d4] $Kn2[g3])
(position)
(position)
(position)
(position)
(position)
(position)
(position $Kn1[g3] $Kn2[d4])
)
)
)
)
)
Här använder jag samma teknik, men skriver explicit ut de sex typer av manövrer jag är intresserad av; detta program är, inte helt överraskande, omkring sex gånger långsammare än det första, men i och med att det arbetar med ett sovrat material känns körtiden inte särskilt betungande. Av den ursprungliga miljonen återstår nu kanske 30-40 träffar.
Det bör noteras att detta bara hittar vita FSPW:er; för att hitta svarta får man köra de båda programmen en gång till, med de båda »taggarna» flyttade till de svarta springarna (dvs byta ut »[N]» i forany-satserna till »[n]»).
Resultat
| Sym | Kort rak | 4 |
| Sym | Lång rak | 4 |
| Sym | Kort diagonal | 1 |
| Sym | Lång diagonal | 2 |
| Sym | Kamelsteg | 6 |
| Asym | Kort rak | 16 |
| Asym | Lång rak | 19 |
| Asym | Kort diagonal | 10 |
| Asym | Lång diagonal | 30 |
| Asym | Kamelsteg | 20 |
När min dator tuggat genom de närmare 5 miljonerna partierna och jag rensat undan dubletter återstod 112 unika partier, vilket tyder på att FSPW-manövern inte är fullt lika ovanlig som man kanske skulle kunna tro. Partierna fördelar sig på de klasser jag definierat enligt tabellen till vänster. Som synes har de asymmetriska FSPW:erna en klar övervikt, och allra vanligast är en asymmetrisk lång diagonal FSPW. Detta beror till en stor del på en ställningstyp som kan uppkomma om man, som svart, ställer upp sig med springarna på d7 och f6 och har e5 under kontroll; sådant kan inträffa i öppningar som kungsindiskt, benoni, volgagambit[5] och förmodligen fler som jag inte kommer på för ögonblicket; och dessutom naturligtvis också i de ställningar där vit ställer upp sig på motsvarande sätt. I dylika fall kan följande inträffa, om spelaren med springarparet har ambitioner att flytta fram positionerna på kungsflygeln:
































































Ställning efter vits 10:e drag
Svart försökte här aktivera sig med 10…Sg4 men efter 11.Sd2 Sge5 12.Le3 Sf6 13.h3 tyckte han uppenbarligen att det var bäst att retirera omedelbart med 13…Sed7, utan att vänta på f4; det hjälpte dock inte, utan vit vann efter 45 drag[6].
Kommen så här långt tänkte jag visa ett urval av de mer intressanta manövrerna; eller kanske mer korrekt, kända schackspelare som dokumenterat sin subtila positionskänsla genom att i något parti utföra en FSPW. Till att börja med tänkte jag visa några »rekord», och vad vore lämpligare än att börja med det först spelade parti jag hittade i min databas; det spelades i en oavgjord match 1856-57[7] mellan de två spelöppningsfarbröderna Bird och Falkbeer.
































































Ställning efter svarts 17:e drag
18.Sfd3 g6 19.Sg4 De7 20.Sde5 h5 21.Sf2 (0-1, 49)
Den tidigaste förekommande FSPW:n i ett parti är samtidigt också det parti mellan de starkaste korrspelarna som uppvisar en FSPW. Vitspelaren, vars fullständiga och magnifika namn var Kornelis Dirk Mulder van Leens Dijkstra[8], var en stark korrstormästare, som bland annat kom delad femma i AE Axelson Memorial, som då den spelades var den starkaste korrturneringen någonsin, med bland annat fyra tidigare och en[9] blivande korrvärldsmästare på startlinjen. Manfred Mädler är kanske inte riktigt av samma kaliber, men är ändå ett känt namn i schackvärlden tack vare sin förlagsverksamhet.
































































Ställning efter vits 6:e drag
6…Sc5 7.b4 Sce4 8.Sa4 Sd7 9.f3 Sef6 (1-0, 52)
Den starkaste spelare som utfört en FSPW är, i det material jag genomsökt, utan tvekan Capablanca, och han gör det med sådan finess och ackuratess att jag valt att ta med ytterligare några drag innan han påbörjar själva FSPW:n. Svart har just flyttat löparen från c8 till d7, vilket möjliggör en synnerligen intrikat springarmanöver. Om den korta datoranalys jag gjorde av ställningen håller, så är det dock inget allvarligt fel; vit kan spela tornet till a1 och plocka a-bonden när han känner för det.
































































Ställning efter svarts 39:e drag
Vits a-springare siktar nu in sig på a-bonden 40.Sc3 Tc5 41.Se4 Tb5 42.Sed6 Tc5 43.Sb7! och där beseglades dess öde. 43…Tc7 44.Sbxa5 Lb5 45.Sd6 Ld7 46.Sac4 och därmed har vit fullbordat sin FSPW. Men han nöjer sig inte med det utan nu följer 46…Ta7 47.Se4! och vit har därmed även fullbordat en sexdragig SPW! I och med bondevinsten var partiet mer eller mindre avgjort, men det dröjde ända till drag 77 innan svart gav upp, och då stod han inför en oparerbar matt, som vit organiserade med hjälp av de två springarna och en dubbelbonde.
Nästa kategori är svår att namnge; den enkla varianten är »vackraste», för att komplettera trion »först, bäst och vackrast», men förutom att sådana påståenden kan dra åt sig ovälkommen uppmärksamhet från F! och likasinnade så innehåller det det orosmoment som består i att jag inte känner till utseendet på de övriga flickor/kvinnor som kvalificerat sig för »Klubb FSPW»[10]. På grund av dessa svårigheter utnämner jag i stället Achmilovskaja till den starkaste kvinnliga spelare som utfört en FSPW.
































































Ställning efter vits 43:e drag
43…Sh7 44.Txf8 Shxf8 45.De3 Sf6 46.Sf2 S8d7 (1-0, 57)
Det var rekordavdelningen. Härnäst följer en uppsättning FSPW:er av stormästare; förutom de ovanstående exemplen har jag hittat inte mindre än sju partier där stormästare var inblandade. Håll till godo!
































































Ställning efter svarts 47:e drag
48.Sbd5 La7 49.Sa6 Lc8 50.Sab4 Lc5 51.Sc7 ½-½
Ska man vara riktigt petnoga hade inte Schmittdiel fått stormästartiteln vid den tidpunkt då ovanstående parti spelades, men att motståndaren var Tal uppväger det mesta.
































































Ställning efter svarts 20:e drag
21.Sf4 Sc6 22.Sfd5 Dd8 23.Se2 Sa5 24.Sdc3 (½-½, 95)
































































Ställning efter vits 17:e drag
17…Sb6 18.a4 Sbd5 19.La3 Sd7 20.Se4 S5f6 (½-½, 61)
































































Ställning efter vits 105:e drag
105…Sb6+ 106.Kc5 Scd5 107.Kb5 Sa8 108.Sb7 Sac7+ (½-½, 112)
































































Ställning efter vits 35:e drag
35…S8h7 36.Ld2 Sd7 37.Kg3 Shf6 38.Kf3 Sf8 (1-0, 81)
































































Ställning efter vits 29:e drag
29…Sb6 30.Dg3 Scd7 31.Lb1 Sa4 32.T4d2 Sac5 (1-0, 38)
































































Ställning efter vits 14:e drag
14…Sb6 15.Sc5 Sbd7 16.Lf4 Sd5 17.Lg5 S7f6 (1-0, 69)
































































Ställning efter vits 21:a drag
21…Sb6 22.Lf2 Sbc4 23.Dc1 Sd7 24.Lf3 Sce5 (0-1, 31)
Så till slut några (fler) svenska exempel. Av de fem inblandade svenskarna har jag bara bekantat mig med två — min före detta klubbkamrat i Kristallens SK, Björn Gambäck, som måste vara en av världens mest aktiva amatörer, och Sollentunas legendariske bingolottoförsäljare Sune Engfors.
































































Ställning efter svarts 21:a drag
22.Sxd4 Lb6 23.Sef3 Lf7 24.Sc6 Lh5 25.Sce5 (½-½, 34)
































































Ställning efter vits 31:a drag
31…Sd7 32.Df3 Sdf6 33.h3 Sf8 34.Te2 S6h7 (1-0, 56)
































































Ställning efter svarts 21:a drag
22.Sd2 Lh6 23.S4f3 Lb5 24.Sb3 O-O 25.Sbd4 (0-1, 55)
Skulle du, mot förmodan, inte fått nog av FSPW:er vid det här laget så har jag lagt upp en pgn-fil med alla 112 partier som jag hittills funnit. Jag lovar inte att jag är färdig med ämnet, men det dröjer nog ett tag innan jag attackerar det igen, även om det finns två stora och intressanta frågor som ännu inte besvarats — har någon i den senaste generationen superstormästare utfört en FSPW, och har det komponerats en studie eller ett problem vars lösning kräver en FSPW? Jag lämnar dessa frågor obesvarade — tills vidare…
Fotnoter:
- Han har dock fler möjligheter; som han skrev om en av dem på Twitter: »Two down, five to go»… [↩]
- Se till exempel det andra temat i Jorge Lois jubileumsturnering [↩]
- Om någon tycker att namnet är så pass träigt att det representerar en brandfara så tar jag med glädje emot bättre förslag i kommentarsfältet. [↩]
- Ett intressant(?) faktum är att de två raka FSPW:erna kan betraktas som »inverser» av varandra; detsamma gäller för de två diagonala, medan kamelstegsvarianten är sin egen »invers». Vad jag menar med detta är att två drag efter den ställning som klassificerar FPSW:n är springarkonfigurationen dess »invers»; detta inses lättast genom att flytta omkring några springare på ett bräde. Från klassifikationssynpunkt spelar detta faktum inte så stor roll i det symmetriska fallet, men i det asymmetriska fallet kan det kanske vara mer berättigat att använda de tre termerna »rak», »diagonal» och »kamelstegs» för att indikera att det inte är så stor skillnad mellan de två varianterna av rak och diagonal FSPW. [↩]
- Rolf Martens gick ju tyvärr bort för några år sedan, så ingen pratar längre om kaijsergambit. [↩]
- Den som inte förstod vad jag pratade om när jag påstod att de två asymmetriska diagonala FSPW:erna på sätt och vis hänger ihop har här en perfekt illustration; om svart i stället börjat med 10…Se5 och följt upp med Sd7, Sg4 och Sgf6 så hade ju hen i stället utfört samma manöver baklänges, vilket var min motivering för att införa begreppet »invers». [↩]
- Det där är min tolkning. Enligt flera källor spelades två matcher, varav den första bara omfattade tre partier (och den andra tretton), men såvitt jag förstår spelades matcherna med ett parti i veckan, och eftersom den »första» matchen påbörjades i slutet av november är det inte orimligt att man helt enkelt gjorde ett uppehåll över jul och nyår. [↩]
- Jag har den största sympati för de stackars redaktörer som genom åren tvingats knöla in detta monsternamn i en tidningsspalt eller liknande begränsade utrymmen. [↩]
- Man skulle också kunna hävda att det fanns två blivande korrvärldsmästare i turneringen, eftersom Tõnu Õim blev världsmästare ännu en gång, i VM-final XIV. [↩]
- Jag måste dock erkänna, att jag av de bilder jag sett på Achmilovskaja på 80-talet, i synnerhet i samband med hennes spionthrillerinspirerade avhopp inför sista ronden i olympiaden 1988, fått intrycket att hon var en mycket attraktiv kvinna. [↩]

Ett första försök, hoppas det inte finns några bilösningar.
Vit: Kg1, Dc3, Th7, La1, Sa2, Sb4, bönder b7, c2. Svart: Kb8, La7, Lh1, bönder b6, b5, d5, g3, g2. Eller som det heter på fackspråk,
1k6/bP5R/1p6/1p1p4/1N6/2Q3p1/N1P3p1/B5Kb w KQkq – 0 1
Självmatt i 4 drag.
Vit måste släppa fram bönderna på b6 och b5 för att tvinga fram avdragsschacken från löparen på a7. Men dessförinnan måste det egna batteriet Dc3-La1 stoppas från att gå emellan:
1. Sc1 d4, 2. Scd3 dxc3.
Springaren på b4 måste stå kvar tills d-bonden är blockerad (svarts b-bönder får inte släppas loss för tidigt) men nu måste den flytta. Enda rutan där den inte senare kan gå emellan på diagonalen a7-g1 är a2:
3. Sa2 b4.
Nu måste b4-bonden stoppas så att b6-bonden blir tvungen att flytta. Samtidigt måste Sd3 undan så att den inte kan gå emellan:
4. Sdxb4 b5#.
Ett trevligt försök, men tyvärr säger Popeye att det finns två bilösningar; både 1.Db3 och 1.Dd3 leder till (själv)matt i fyra. Det verkar inte helt omöjligt att få bort dem; jag prövade den enkla varianten att byta plats på dam och löpare, men då finns 1.Dd1. Men som som sagt, det borde gå…
Ja jäsiken. Kul att du prövade att byta plats på dam och löpare, det var så jag hade från början. Hjälper det att ställa bönder på a3 och b3? Det där Popeye ska visst vara gratis säger de, men jag förstår inte hur man installerar det (på mac). Har du något tips?
Jag har inte använt Mac särskilt mycket de senaste 20 åren, eller så, men jag hittade den här sidan, som tyder på att det borde gå på något sätt. Popeye är i grunden ett textbaserat system, så i Windows öppnar man ett kommandofönster och skriver ”pywin32 < input.inp", där pywin32 är programmet och input.inp en fil som beskriver problemet; den jag använde ser ut så här:
beginproblem
author Johan W
origin ???
protocol johan1.out
stipulation s#4
option movenumbers
pieces white Kg1 Bc3 Rh7 Qa1 Sa2b4 Pb7c2
black Kb8 Ba7h1 Pb6b5d5g3g2
endproblem
(Notera att springare heter "S"; "N" är nattryttare…!)
Jag gissar att man gör något liknande i Mac; men exakt hur det går till har jag ingen aning om. Lycka till!
Ha! Nu har jag fått det att fungera, och tack för springarna, med nattryttare blir det ingen matt! Nu säger den att med vita bönder på a3 och b3 är min tänkta lösning den enda!
Dubbelt grattis! (Det verkar som det inte finns fler svarsnivåer just nu, vilket kanske är rimligt med tanke på att kolumnbredden minskar för varje svar…) Då är det bara att skicka in problemet till Springaren och hösta in ovansklig ära…