Någon gång i den här bloggens barndom lovade jag — eller hotade, om man ser det från en annan vinkel — att återkomma med en analys av en studie som var snarlik en som diskuterades i den aktuella bloggan. Detta löfte/hot kan nu sättas i verkställighet sedan jag hittat den ställning det handlar om. Den ser ut så här:























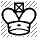








































Chéron och Ward
Den som råkar ha ett exemplar av Pachmans bok »Endspielpraxis im Schach» återfinner den som diagram 203 på sidan 144[1], och det dubbelfel som jag antyder existensen av i rubriken har jag redan påtalat i en krönika i Corren, sannolikt publicerad i början av juni 1987[2]. Jag kommer att skriva några ord om bakgrunden till den krönikan innan jag tar plockar fram rödpennan, så du har här ett förträffligt tillfälle att förbättra ditt självförtroende genom att hitta fel som slutspelsexperter, stormästare och bosjo förbisett. Plocka fram ett bräde, ställ upp ställningen, och besvara frågan »vinner vit, och i så fall hur?»
När jag skrev krönikan i Corren hade Axel Ornstein orsakat ett viss rabalder i schackkretsar genom att hävda att det fanns fel i åtminstone hälften av alla publicerade studier. Jag har inget minne av att ha sett Axel’s artikel, men den diskuterades en hel del, dels av de som tyckte att det där med att lösa studier var bortkastad tid och nu fick vatten på sin kvarn, och dels av de som tyckte Axel var helt fel ute. Den ilsknaste kommentaren från det senare lägret stod förmodligen Alexander Hildebrand för i TfS (se sidan 386 i länken ovan). Utan att agera domare i frågan kan man nog hävda med visst fog att Alexanders tvärsäkra procentsatser i TfS nästan säkert är för låga; som ett exempel på en mer realistisk uppskattning kan man ta John Nunns redogörelse för hur han sållat ut omkring 2500 studier som kandidater för att användas i sin bok »Endgame challenge», men att han fann att mer än tusen av dem hade defekter. Åkej, det är inte riktigt 50%, men jag vill minnas att Axel i något sammanhang påpekat att han menade fel i en bredare bemärkelse, inte bara felaktiga och/eller bilösliga studier, så jag lutar nog ändå åt att Axel låg närmare sanningen än Alex.
Dags att plocka fram rödpennan för att kludda lite rättelser i ditt exemplar av »Endspielpraxis im Schach». Svaret på frågorna ovan är »Javisst!» respektive »Nästan hur som helst, bara hen inte sätter patt eller tillåter svart att slå g-bonden»; detta är ju numera lätt att verifiera genom att konsultera Nalimovs databaser på webben. Enligt Pachman så ville Chéron och Ward vinna med följande manöver: 1. Kg5 (Detta är tvunget; på alla andra drag spelar svart 1…Sf5+! med omedelbar [2. Lxf5] eller nästan omedelbar [2. Kg5 Se7, följt av Sxg6] remi) 1…Se8 2. Ld7 Sd6 3. Kf4?! (Ett litet avsteg från den snabbaste vägen, men vinsten är inte bortspelad än.) 3…Kg7 4. Ke5??? Sc4+??? 5. Ke6 Se3 6. h8D+! Kxh8 7. Kf6! (Gissningsvis var det denna finess Chéron ville visa; 7. Kf7 direkt leder bara till remi) och vit vinner. Men som mina frågetecken indikerar finns det ett gigantiskt hål i varianten — svart spelar ju 4…Kxg6!, eftersom svart har en springargaffel på f7 om vit spelar 5. h8D. Enligt Pachman påpekade en A. Eck från München detta, och märkligt nog låter han saken falla där. Dags att lämna ordet till bosjo, årgång -87:
Men titta på ställningen en gång till, glöm bort att det handlar om en studie[3] och använd i stället »sunt förnuft»: Vit har två bönder mer, bättre kungsställning och en stark löpare mot en dålig springare. Slutsatsen är självklar: Vit »måste» stå på vinst! Det gäller bara att se till att svart inte kan offra hästen för g-bonden, som i varianten ovan. T ex 1. Kg5 Se8 2. Ld7 Sd6 3. Lc6! vinner snabbt i alla varianter: På springarflytt vinner vit pjäs direkt eller sätter matt (Kh6 följt av g7) och på 3…Kg7 vinner 4. h8D+! Kxh8 6. Kf6 lätt. Inte heller kan svart rädda sig på annat sätt, 2…Sg7 3. Kg4!, 2…Sc7 3. Kh6! eller 2…Sf6 3. Lb5! Sxh7 4. Kh6! demonstrerar tydligt vits positionella övertag. Sunda förnuftet har återigen fått sista ordet!
Av skäl som jag strax kommer att redovisa håller jag Ward för oskyldig till eventuella kalamiteter, så hittills har vi placerat Chéron och Pachman i skamvrån för att ha missat en remiväg respektive en enkel teknisk vinst. I en tidigare fotnot påpekade jag att jag hittat ett par-tre missar till. En av dem får gissningsvis tillskrivas ett överhoppat drag-par av sättaren och en sovande korrekturläsare; i varianten med 2…Sf6 anger Pachman »4. g7+», vilket inte bara är regelvidrigt utan också skulle satt bort bonden. En annan ganska lustig miss gör Pachman efter 2…Sg7 då han låter vit spela 3. Kf6, för att några drag senare nå fram till samma pjäsvinst som efter 3. Kg4, fast nu med löparen på g4 och kungen på e7.
Men tyvärr kommer jag[4] nog inte undan en stund i skamvrån — efter 2…Sc7 är 3. Kh6?! förvisso inte förtjänt av något utropstecken. Visserligen skulle jag med viss möjlighet att bli trodd kunna hävda att det var Correns närsynta sättare som inte kunde se skillnad på »f» och »h», men om jag menade att skriva 3. Kf6 borde jag fortsatt varianten några drag till — efter till exempel 3. Kf6 Se8+ 4. Ke7 Sf6 är det bara 5. Kf7! som vinner. Eftersom jag är en snäll rättare skulle jag dock inte ge något poängavdrag för den missen, men ett minustecken i kanten blir det definitivt. Och nog borde jag påpekat att hästen kunde »rökas ut» från sitt blockadfält på g7 med hjälp av dragtvång; utan den finessen kan vit inte komma vidare, vare sig med sunt förnuft eller på något annat sätt; ännu ett litet minustecken i kanten.
![]()
Som jag påpekat ovan är jag inte längre säker på att detta är en studie, och anledningen till det är att jag hittade följande ställning i den andra volymen av Chérons klassiska »Lehr- und Handbuch der Endspiele»[5]:
































































Analyser av W. Ward och Chéron
Rubriken hade dessutom upplysningen att ställningen var hämtad från ett parti som spelats i Lancashire 1915. Ställningen är vald som ett exempel på ett undantag från den generella regel som säger att i ett slutspel med L+2B vs S, där bönderna är förbundna, måste bönderna avancera på rutor av motsatt färg till löparen så att inte springare och kung kan blockera bönderna utan att löparen kan bryta blockaden. Som Chéron helt riktigt påpekar, och du förhoppningsvis kommit underfund med själv här ovan, finns det undantag från den regeln om springaren bara har fyra fält till sitt förfogande, så att den starkare parten kan använda dragtvång för att forcera fram bönderna.
Exakt vad som hänt har jag inte listat ut, men en rimlig gissning är väl att Ward kommenterade partiet strax efter att det spelats[6], att Chéron skrev om ställningen långt senare, och så småningom tog med den då han samlade ihop material till sin »handbok». Hur den felaktiga version som Pachman publicerade har uppstått är ännu höljt i dunkel — framför allt har jag svårt att förstå att en erkänt skicklig analytiker som Chéron skulle ha gjort ett sådant elementärt fel — men troligen såg Chéron finessen i 7:e draget i den avsedda lösningen, och slarvade med detaljerna när han försökte göra en studie av ställningen. Jag har dock inte funnit ställningen vare sig i den (första) upplagan av van der Heijdens databas eller i någon annan bok eller databas, så eventuella bloggbesökare med stora schackbibliotek och databaser får gärna fortsätta forskandet.
Fotnoter:
- Jag brukar hävda att jag inte läser mina schackböcker, utan nöjer mig med att veta att jag har dem, men här tyder ett antal markeringar med en blå överstrykningspenna på att jag i alla fall öppnat boken. [↩]
- Vid närmare påseende kan man hitta åtminstone fyra-fem enkla förbiseenden i den här sorgliga historien, varav ett tycks vara gjort av mig. Jag kommer att försöka bortförklara det senare. [↩]
- Där har jag eventuellt fel; se nedan. [↩]
- Eller rättare sagt bosjo, modell -87. [↩]
- Jag införskaffade serien trots att Robert Danielsson avrått mig; hans motivering var att den var helt oläsbar. Han hade naturligtvis rätt i det; men det går utmärkt att slå upp saker i den samt bläddra på måfå bland studierna. [↩]
- Om W. Ward är den jag tror dog han enligt uppgift 1920. [↩]





